Проведите две прямые линии, разбив греческий крест на 4 одинаковые по форме и размеру фигуры, из которых впоследствии можно сложить квадрат.

Ответ: Прямые АБ и ВГ проводятся между центрами соответствующих сторон греческого креста.
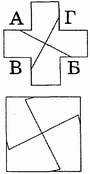
Проведите две прямые линии, разбив греческий крест на 4 одинаковые по форме и размеру фигуры, из которых впоследствии можно сложить квадрат.

Ответ: Прямые АБ и ВГ проводятся между центрами соответствующих сторон греческого креста.

Комментарии
На испанском МЕНСА - переводится как ДУРА. Поэтому мало испанцев в этом обществе.)
На улице дождь, я сижу дома, где находиться афроамериканец в данное время?
если я переступлю через кирпич?
PS.2% идиотов от общего числа. НЕ НУЖНО ВВОДИТЬ ЯЗЫКОВУЮ ИЛИ ИНУЮ ЭКСПЛИКАЦИЮ НЕЯСНОЙ ЭТИМОЛОГИИ, IQ ТЕСТ - НЕ СВЯЗАН С ИНТЕЛЛЕКТОМ, ДОКАЗАНО СЦИЕНТИЗМОМ!
А вот ерундой маяться - сциентизмом не доказано, поэтому 2% и маются ерундой!
я вообще про женский цикл думала
ну у кого что болит
что-то не припомню ни одного выдающегося испанского математика, физика и т.п.
может потому что их попросту не было.
если кто знает таких, напишите.
а я разделил по другому и получился
квадрат полый внутри
Аналогичное решение...разделив крест по вертикали и горизонтали )
+1. Условие нечётко задано, варианта может быть как минимум два.
И у меня тоже самое.Делится по центру по вертикали и горизонтали и складывается квадрат с пустотой внутри.
объясните мне как из этой закорючки получается квадрат!!!!
А никак. Тупая задача, тупое решение. Тупость тупость, ты моя отрада. Ткпость, тупость, ты моя услада. (Брехт)
Квадрат получается , проверено эмпирическим путём. Хотя детали приходиться слегка подогнать, то есть наложить одну на другую.
меня в этой задаче сильно удивило, когда при складывании xfcntq начала образовываться свастика. очень мило
помогает в решении данной задачи следующая логика:
из пяти квадратов надо получить один, следовательно его сторона будет равна sqrt(5) (корень из пяти), чтобы сложить данный квадрат из четырёх одинаковых фигур, у фигур должна быть хотя бы одна сторона равная sqrt(5)/2. При этом нужно чтобы в фигуре имелся прямой угол.
Чтобы разделить греческий крест на четыре одинаковых фигуры
2-мя прямыми, нужно сначала разделить его на две части, а потом другой прямой ещё на две, причём в любом случае в центре углы прямые.
Теперь остаётся только найти отрезок, длина которого равна sqrt(5)/2, что не составляет большого труда, зная что он проходит через центр!