Астронавт высадился на экваторе астероида, имеющего форму шара. Он прошел на север 100 км (не достигнув полюса), затем прошел 100 км на восток, далее повернул на юг и прошел еще 100 км. В итоге он оказался на 200 км восточнее точки высадки. Сколько километров ему еще надо пройти на восток, чтобы оказаться в первоначальной точке?
Ответ: Найдем длину экватора астероида.
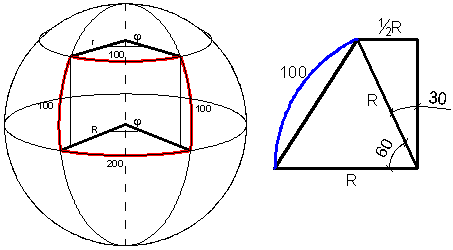
На первом рисунке: r*phi = 100, R*phi = 200 отсюда r/R = 1/2
Из второго рисунка: 100=π/3*R, поэтому R = 300/π
Зная радиус астероида, находим длину экватора: 2*π*R = 600 км
Т.е. астронавту надо пройти на восток еще 400 км.
Обсуждение задачи на форуме: Астронавт на астероиде

Комментарии
я зауважал стереометрию!!!!!!!!!!!!!!
ничеее не понила(((((((
Рис 1 - заведомо неверен. Нельзя по нему работать. Представьте просто треугольник, у которого основание 200 а стороны - меридианы. Углы м\д сторонами и осн. равны =} треуг. - равнобедренный. Он, кажется , на восток 100 прошагал - так это же 1\2 от основания =} до полюса ещё 100 осталась =} и стороны и основание по 200. Что, уже догадались? нужно помнить, что мы брали проекцию на плоскость, а значит углы подле основания искажались....я дурак!
я тоже зауважал "стереометрию" )))
а у меня по моим расчетам получалось 1000 км..((
неправильно задача решена! на рассмотренном рисунке угол фи не равен будет 60 градусов. он будет 90.астероид круглый, следовательно его экватор и окружность, проходящая через полюса параллельно меридианам равны. расстояние от экватора до полюса будет 200км - а это только четверть окружности, следовательно вся она будет 800, а пройти ему осталось 600 на восток.
А у меня тоже получилось 600 только по другому...
если действительно астероид имеет формуидеального шара, то 100 км пройденых насевер будут составлять 1/8 окружности, т.к. если провести линии до севера как раз получится равнобедренный треугольник. Следовательно если астронавт оказался восточнеена 200 км восточнее от точки высадки ему останется пройти 800км-200км = 600. Это наверное примитивная логика однакомнекажется верная.
мой ответ: автор плохо учился в школе, точнее хорошо учился, но все забыл!
итак ответ: 1000 км
В итоге он оказался на 200 км восточнее точки высадки. Сколько километров ему еще надо пройти на восток, чтобы оказаться в первоначальной точке? - в задаче ответ уже есть!!!а там считать чего-то все начали!!!
На восток а не на запад.
Ответ правильный. Только со второй частью намудрили.
Из второго рисунка видно, что 100 км = 1/6 окружности. Значит 600-200=400
В процессе расчёта получается, что дуга в 200 км является четвертью всей окружности. В 6 комментарии пользователь также выдвигает этот факт, но почему-то противоречит своим словам в ответе. Если, 200 это 1/4, то вся длина=800 км. 200 он прошёл, осталось 600км.
Точнее, не в 6# комментарии, а Валентин Сергеевич. Нумерация пунктов с каждым ходом меняется.))))
С таким условием, задача имеет много решений.
Утверждение "отсюда r/R = 1/2" - ошибочно, так как это частный случай.
Правильное соотношение верхнего и нижнего радиусов r=R*cos(100/R) (в радианах)
Например:
R=70.676км
r=10,973км
угол ф1 = 162,1365 градусов (на экваторе)
угол ф2 = 522,1365 градусов (около северного полюса)
(двигаясь на восток астронавт сделал один полный оборот)
осталось до точки старта 244,07 км
можно посчитать на два и более оборотов при движении на восток
Товарищ!! не смотри на рис.1, он тебя сбивает с толку, угол phi при любом раскладе, по определению в задаче, не может быть разным для экватора и для другой любой параллели, в данном случае phi = 120 градусов. Каким способом люди тут нашли экватор 800 км - не понятно.
Если r это радиус астероида, а n (0, 1, 2 ..) - количество целых оборотов, что астронавт сделал на востоке, то все возможные радиусы находятся из уравнения
cos(100/r) * (2*pi*n*r + 200) = 100,в пределах
(200/pi; 300/pi], где оно имеет одно решение.согласен с длиной экватора равной 800 км
Длина экватора 600 км, задача решается в уме
600 км
По-моему, у задачи нет решения: ведь не известны ни радиусы, ни углы. Всё что мы имеем - длины дуг, что недостаточно для применения формулы L=r*φ. В итоге задача получается с двумя неизвестными.
2й рисунок вообще ни к месту: откуда взялись ½R и углы в 60° и 30°?
Откуда взялась формула 100=?/3*R? Видимо, "автор" с какого-то перепугу решил применить формулу Гюйгенса p=2l+(2l–L)/3, хотя она тут вообще не применима...
Беру свои слова обратно. С Гюйгенсом меня занесло.
Посчитал сам - сошлось с ответом. Длина экватора 600 км.
А "автору" в ответе следовало бы указать откуда 60° взялось (а то вон народ дебаты устраивает, вместо того чтобы с ответом согласиться).
А как угол 60 градусов посчитали не могу понять?
треугольник на рис.2 является равносторонним
как 60 градусов высчитали?
Я вообще понять не могу откуда какие формулы и все такое
Изначально условие задачи не правильное "В итоге он оказался на 200 км восточнее точки высадки. Сколько километров ему еще надо пройти на восток"
Если написано что он оказался на 200 км восточнее то скока ему на восток надо пройти?
народ все дело в дугах! задача поставлена коректно и прав тот кто говорит что это частный случай это из условия вытекает. просто есть зависимость в окружностях. внимательно посмотрите условие!!! углы фи равны а дуги относятся как 1 к 2 тоесть вторая окружность меньше экваториальной в 2 раза следовотельно и радиусы относятся так же! просто нкжно подумать ответ 400
все верно, но тогда правильный ответ 600, вопрос звучит сколько осталось пройти на восток по экватору.
Задача имеет бесконечное количество решений
Правильный ответ выглядит как алгебраический ряд. на первый взнляд ряд имеет следующие характеристики: отрицательный тренд, а1=400, an стремящеся к +0, ряд имеет ограниченное число членов
Все зависит от того на сколько близко астронавт подошел к точке полюса в первой точке поворота и сколько витков (кругов) он прошел двигаясь на задорной широте на восток
что за бред вы несете!
все верно, даже из логических размышлений. 100 км, которые чел идет на восток, мог идти, наматывая круги, если это близко к полюсу.
Уважаемые знатоки! Прежде всего надо понимать, что у малого и большого сегментов опорный угол одинаковый, а радиус малого сегмента в два раза меньше большого, так вот подставьте углы и узнаете правильный ответ.
Господа, я конечно прошу прощения, но кто-нибудь заметил ошибку в расчете?
"Из второго рисунка: 100=?/3*R, поэтому R = 300/?"
Вообще-то 200=п/3*R.
И пораскиньте мозгами - у Вас угол п/3 - это 60 градусов, сколько раз 60 градусов укладывается в 360??? а не 180!!!
200*6-200(на которые он уже восточнее)=1000 км ему нужно пройти на восток!!!
"В итоге он оказался на 200 км восточнее точки высадки. Сколько километров ему еще надо пройти на восток, чтобы оказаться в первоначальной точке?"
"Точка высадки" и "первоначальная точка" так то одно и то же.... ответ 200км
неправда!!! радиус экватора = 360 градусов , следовательно его делим на 6 частей по 60 градусов, это получается на каждые 60 градусов= 100км : 100х6= 600. 600-200=400 км, ему осталось пройти на восток 400км.
Диаметр 800 км, осталось пройти 200 км.
У меня получилась длина экватора 800 км, и осталось пройти 600 км. Без сложных рисунков, путь в 100 км по меридиану дает приращение по экватору на восток в 50 км, потом 100 км по параллели, и опять вниз по меридиану, еще 50 км плюс по экватору. Из середины отрезка экватора в 200 км проведем меридиан до северного полюса, получится 200 км длина меридиана до полюса, это 1/4 длины окружности, значит длина экватора 800 км.
Дамы и господа. Прежде чем спорить и доказывать просто возьмите и нарисуйте две окружности с общим центром и радиусами один больше другого в два раза и все станет ясно. При условии задачи если поднявшись по меридиану диаметр круга уменьшается в два раза ( а это видно из условия когда он обратно по меридиану спускается вниз то длина окружности пройденной увеличивается в два раза) то расстояние пройденное им по параллели, то есть 100 км., должна составлять 1/4 окружности по этой параллели. Соответственно длина всей окружности равна 400 км. А так как длина окружности по экватору в два раза больше то она равна 400*2=800км. Соответственно пройдя по экватору 200 км. пройти до начальной точки остается 600км.
Да, прекращайте вы уже! Правильный же ответ дал автор! И вообще можно решить чисто аналитически. Точка на поверхности шара определяется уравнение x2+y2+z2 = R2, где x,y,z - прямоуголные координаты (в частности z - высота), R - радиус планеты. Для радиуса в плоскости, параллельной экватору, r на определенной широте r2 = x2 + y2, тогда получается r2+z2=R2. Здесь z напрямую нельзя использовать как 100 км!!!, т.к. путь астронавтра криволинейный!! - по дуге окружности, его путь S=R*phi (phi в радианах - широта, угол по вертикали от центра планеты до точки в плоскости перпендикулярной плоскости экватора). высота до точки 1, куда шел астронавт по мерилиану, от плоскости экватора z = R *sin(phi). Подставляем в уравнение и получаем r2=R2-z2=R2(1-sin2(phi) )=R2*cos2(phi), отсюда r=R*cos(phi). мы знаем, что соотношение между радиусами 1/2, тогда получаем, что cos(phi)=1/2, тогда получаем, что phi - Pi/3 радиан! т.е. космоноват прошел по меридиануPi/3 радиан широты, и его путь составил 100 км. исходя из формули для его пути, а именно R = S/ phi, получаем радиус планеты R =100км / Pi/3. длина экватора - длина окружности радиуса R - есть D=2*Pi*R = 2*Pi /Pi*3 * 100 = 600 км. Так как астронват прошел 200 км, идет на восток, и ему нужно вернуться в туже точку, ему нужно пройти еще 600-200=400км.