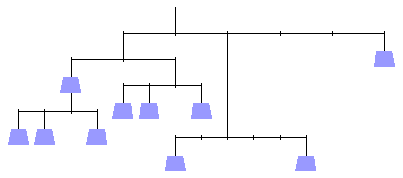
Необходимо распределить 10 гирь, имеющих вес от 1 до 10 кг. в сиреневые чашечки этих необычных весов, чтобы вся система оказалась в равновесии:
Ответ:
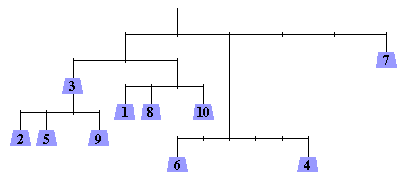
Необходимо распределить 10 гирь, имеющих вес от 1 до 10 кг. в сиреневые чашечки этих необычных весов, чтобы вся система оказалась в равновесии:

Ответ:

Комментарии
Может возможно подобрать ещё варианты решений...
Голые ответы это не ответы. Гораздо интересней было бы узнать метод, по которому эти цифры были высчитаны. Не подбором же в конце концов это делалось.
Тут надо знать еще и физику, или теоретическую механику.
Учитывать плечо.
Давно это было, ща просто так без справочника не вспомню формулу.
??? не понятно как получилось
PS 2 с 3 не перепутали случайно?
спасибо, убил мозг, но решил)
Решил с помощью расчетов, все можно обосновать.
Если интересно напишу.
Хунта полная!
Действительно, как решать?Составил систему уравнений, но неизвестных гораздо больше чем уравнений. Видимо распределять нужно методом тыка, выбирая самую тяжелую гирю и самую крайнюю. Подскажите ход решения, пожалуйста. Всем интересно стало))
Обозначим: Номера весов - сверху вниз (весы №1 сверху, весы №5 самые нижние).
Массы грузов- слева направо х2,х3,х1,х4,х5,х6,х7,х8,х9,х10
(для проверки:
на весах №1- весы№2, весы№5,гиря х10
на весах №2- весы№3, гирях1+ весы№4
на весах №3- гири х5,х6,х7
на весах №4- гири х2,х3,х4
на весах№ 5- гири х8,х9 )
1. В задаче предполагается, что все гири имеют целочисленную массу и среди них нет гирь с одинаковой массой (т.е. есть 10 гирь с массой 1,2,3…10 кг)
2. Введем обозначения для масс гирь (см. рисунок). Обозначим х5+х6+х7=a, х8+х9=b,
3. Суммарный вес всех гирь S=1+2+3+4…+10=55 кг.
4. Из равновесия равноплечих весов №2 следует что их суммарная масса =2а, тогда 2a+b+c=S=55 (1). Из соотношения плечей весов №1 следует 2a=b+4c (2). Из (1) и (2) следует b= 2.5(11-с). Для всех с=1…10 определим все целочисленные b. Т.к. b=x8+x9 то b<=19. Таким образом подходящими являются с=5, b=15; c=7, b=10; с=9, b=5. Из (1) a=(55-b-c)/2, подставляя пары (с,b) определим что «a» является целочисленным только при c=7, b=10 (при этом a=(55-7-10)/2=19). Таким образом с=х10=7.
5. Из равновесия весов №5 следует 2*х8=3*х9, и т.к. х8+х9=b=10 находим x8=6, х9=4.
6. Из равновесия весов №3 следует 2*х5+х6=х7. Т.к х5+х6+х7=a=19 получим х5=2*х7-19. х7 может быть равен только 10 т.к. при любом х7<10 x5 будет отрицателен. Таким образом х7=10, тогда x5=1, х6=8.
7. Остались неопределенны места для гирь с массами 2,3,5,9.
8. Из равновесия весов №4 следует х4=2*х2 +х3. х4 может быть равен только 9 (т.к. остальные значения массы просто не подходят), тогда х2=2, х3=5
9. Осталось х1=3
10. Ответ х1=3, х2=2, х3=5, х4=9, x5=1, х6=8, х7=10, x8=6, х9=4, х10=7.
полностью с тобой согласен ход мыслей у меня был именно таким(5 комментарий), решение также только одно единственное и по другому его просто не решить, кто смог решить эту головоломку тому большой респект!
по моим подсчетам весы не все в равновесии, главные не уравновешены оказались
P.S а как уравновесили 6 и 4 ? хахах)))
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55 кг
В теории можно забить на все дочерние весы и не пытаться их уравновешивать по отдельности, потому что цель уравновесить систему, а нее ее фрагменты.
55 / 2 = 27.5 кг.
т.е. 27.5 кг на каждую сторону.
гирь по 0.5 у нас нет.
Но если присмотреться - центр весов проходит через одну гирю, в ответе на этой гире висит номер 6.
Если на нее повесить 1, то на каждую сторону мы получим по 0.5 кг.
А дальше просто:
2 + 3 + 4 + 5 + 6 + 7 = 27 кг - все это вешаем слева пофик как.
8 + 9 + 10 = 27 кг - вешаем с права пофиг как.
Все - решено.
Задача не сложная.
А в ответе - ошибка, если я конечно со своим решением не профтыкал.
Потому шо с права 10 + 4 + 7 и еще + (6 \ 2) = 24 кг. С лева перевес на 3.5 кг.
а еще было бы круто, если бы нужно было учитывать вес креплений ))
а я решил)
1) отталкивался от того что сначала надо найти значения для плеча снизу справа
подходят значения 3 и 2; 6 и 4; 9 и 6
2) потом для того что правей всех, чтобы выполнялось самое первое равенство(то которое выше всех), это 9 для первой пары; 7 для второй и 5 для третьей
3) тк левое верхнее плечо имеет два деления одинаковых значит цифра должна быть кратна 2; соответственно значения 3+2+9(*4)=41 и 9+6+5(*4)=35 не подходят. Теперь извесно что в правом плече снизу будет 6 и 4 а в самом правом 7
4) теперь задача намного проще, осталось левое плечо весом 38кг, разделено на 2 ровных части (по 19 каждая)
5) есть два одинаковых плеча 2х+у=z, при оставшихся числах это может быть только 3(*2)+2=8; 2(*2)+5=9 или 1(*2)+8=10 к тому же известно что правое плечо должно быть в сумме 19кг, соответственно это может быть только третий вариант
6) после того как узнали правое плечо первый вариант отпадает (тк восьмёрка уже используется) соответственно лево плечо будет 2(*2)+5=9 ну и остаётся одно место для 3кг, проверяем (2+5+9 нижнее левое плечо)+3=19кг
уравнение решено :)
попробую по короче
(№1+№2+№3+№4) + (№5+№6+№7) = (№8+№9) +4 * №10
(№1+№2+№3+№4) = (№5+№6+№7)
нечет. + нечет. = чет. => (№8+№9)=чет.
чет. + чет. = чет. => (№8+№9)=чет.
=> №10= нечет.
№8 и №9 = 3 и 2 или нечет. + 4 * №10 = нечет. пусто
= 6 и 4 или чет. + 4 * №10 = чет. правда
= 9 и 6 нечет. + 4 * №10 = нечет. пусто
№8 и №9 = 6 и 4
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55 кг
1 + 2 + 3 + 5 + 7 + 8 + 9 + 10 = 45 кг
(№1+№2+№3+№4) + (№5+№6+№7)= 45 кг-№10 -№8 - №9 =>
= 35 кг - №10 = 4 * №10
=> 35 кг = 5 * №10
=> №10 = 7 кг
=> (№1+№2+№3+№4) + (№5+№6+№7)= 55 кг-6 кг-4 кг-7 кг
=> (№1+№2+№3+№4) + (№5+№6+№7)= 38 кг
=> (№1+№2+№3+№4)= 19 кг (№5+№6+№7)= 19 кг
=> (№5+№6+№7) 1+8+10 однозначно
=> (№1+№2+№3+№4) будут остальные 2,3,5,9, при том,
=> 2 * №1 + №2 = №4 однозначно
=> №1 = 2 однозначно
№2 = 5 однозначно
№3 = 3 однозначно
№4 = 9 однозначно
другого не может существовать