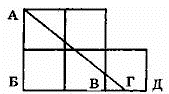
Фигура состоит из 5 одинаковых квадратов. Необходимо разделить ее одной прямой на две равные по площади части:

Ответ: Проведем линию от точки А до точки Г так, точка Г делит отрезок ВД пополам. Если принять сторону квадрата за единицу, то площадь пяти квадратов равна 5. Найдем площадь треугольника АБГ. SАБГ = 0,5*АБ*Бг = 0,5*2*2,5 = 2,5, т.е. ровно половина площади исходной фигуры

Комментарии
Можно взять один из квадратов со второй вертикали, разделить горизонтальную сторону пополам, левый отрезок ещё раз поделить пополам и провести вертикальную линию через получившуюся точку - будет так же 2.5 квадрата по каждую сторону от прямой.
Суть такова: Линия проходящая через точку пересечения диагоналей(в данном случае) квадрата и прямоугольника делит выш. упомянутые фигуры на две категорически равные по площади фиговины. Таким образом, если мы раздели две фигуры(квадрат и прямоугольник либо два квадрата, либо два прямоугольника), каждую пополам, а потом сопоставим суммы площадей половины первой фигуры и половины второй фигуры с суммой двух других половин, то ВНЕЗАПНО обнаружится, что эти суммы равны.
Способ 1.
Принимаем два верхних квадрата за прямоугольник №1 со сторонами 1 ед и 2 ед.;
Проведем диагонали этого прямоугольника №1, а точку пересечения обозначим как А;
Принимаем три нижних квадрата как прямоугольник №2 со сторонами 1 ед. и 3 ед.;
Проведем диагонали этого прямоугольника №2, а точку их пересечения обозначим как В;
Проведем прямую проходящую через точки А и В, эта прямая разделит первоначальную фигуру на две равные по площади части.
Способ 2.
Условно достроим первоначальную фигуру до прямоугольника со сторонами 2 ед. и 3 ед;
Проведем диагонали этого прямоугольника, а точку их пересечения обозначим как С;
Выдели, в полученном ранее прямоугольнике, фигуру заданную первоначально, что позволит нам отсечь, от полученного ранее прямоугольна, квадрат со стороной 1 ед;
Проведем диагонали этого квадрата, а точку их пересечения обозначим как D;
Проведем прямую проходящую через точки C и D, эта прямая разделит первоначальную фигуру на две равных по площади части.
Способ 3.
Все примерно тоже самое, но на этот раз выделяем крайний правый квадрат в нижней горизонтали как отдельную фигуру, а все остальные квадраты условно объединяем в один большой со стороной 2 ед. проводи диагонали получившихся фигур и тд. и тп.
Не могли бы пояснить суть и правомерность Способа 2? А то этот способ как-то не очень укладывается в рассуждения, приведенныё в начале вашего поста. Ибо Вы об отсутствующей фигуре рассуждаете точно так же, как о реальной, не обосновав, что так можно делать.
гениально
Способ 3 - лучший!
это решение правильнее и проще!
Халтура!
Если и считать такое решение верным, то лишь после дополнительных построений - повторений исходной фигуры таким образом, чтобы линия шли по диагоналям клеток.
Аналогично Вашему способу можно предложить такой: проведем вертикальную черту на расстоянии 1.25 клетки от левого края.
Все решения, где нужно что-то вычислять или делить пополам - очень плохие, сложные и непрактичные. Нужно обойтись одной только линейкой без делений. А если можно складывать бумагу, то даже и без линейки.
Самое "правильное" решение упомянуто ниже в "Опубликовано Гость в Вс, 12/08/2013 - 04:02." номер 3, потому что требует наименьших действий. Я его переформулирую и покажу, что в этом способе требуется всего 2 вспомогательные линии:
Шаг 1-ый - берём большой квадрат, образованный 4-мя левыми квадратами. В нём уже обозначена точка его центра, так что с нам ничего делать не надо.
Шаг 2-ой - берём оставшийся маленький самый правый квадрат, проводим (лишь с помощью линейки) его диагонали и так находим его центр.
Шаг 3-ий - проводим линию через эти 2 точки (центры большого и маленького квадратов).
Теперь, на всякий случай, еще раз суть метода, описанного в "Опубликовано Гость в Вс, 12/08/2013 - 04:02." другими словами. У любой геометрической фигуры есть центр. И если через этот центр провести любую линию, то она разделит фигуру по площади пополам. Если у нас есть 2 фигуры, то одна линия, проходящая через центры этих фигур, будет делить сразу обе эти фигуры пополам. А значит, будет делить и совокупность этих двух фигур пополам.
В случае этой задачи, нужно разделить сложную фигуру на две простых, у которых легко найти центры. И провести через них линию.
Нижний квадрат разделить пополам, и половинку поднять наверх. Получится в ряд (сверху) - два квадрата с половиной. Проводим вертикальную линию , отмеряя один квадрат и еще 1/4 квадрата. Площади полученных фигур будут равны. Высоты одинаковые- два квадрата, основания получившихся двух прямоугольников- 1,25 стороны квадрата.
Зачем переносить половинки? Можно сразу отрезать вертикальной линией, отступив 1 , 25
Для решения находим середину верхней стороны верхнего правого квадрата(точка "А") и соединяем её с серединой нижней стороны большого квадрата(состоит из 4-х малых). Всё - решение готово! Слева 2,5 квадрата, а значит справа тоже 2,5.
Похоже, задача имеет не одно решение. У меня получился другой вариант: Линию можно провести из нижнего левого угла центрального квадрата в нижнем ряду...до середины верхней стороны правого квадрата в верхнем ряду.
Здесь действительно есть много вариантов решения.
Если есть только линейка без делений, то можно провести эту линию так:
1) Чертим диагонали левого нижнего квадрата.
2) От точки их пересечения проводим перпендикуляр к левой вертикальной стороне этого же квадрата. Получаем точку, являющуюся центром стороны.
3) Точка Б - это правая верхняя вершина нижнего центрального (соседнего) квадрата. Она уже есть на рисунке. Отрезок АБ делит исходную фигуру на две равные части, площадь каждой из которых равна 2,5 квадрата.
Забыл сказать: точка А - центр стороны, к которой проведён перпендикуляр (шаг 2).
Представленное решение понятно. Имеется фигура площадью 5 кв.ед. Нужно отсечь фигуру площадью 2,5 кв.ед - и самое простое что приходит на ум это треугольник со сторонами 2 и 2,5 ед. Он прекрасно размещается в представленной фигуре и вроде бы все хорошо. Но вот реализация этого решения, а именно нахождение точки Г, требует инструмент. А существуют более простые решения которые не требуют измерений.
Ответ Гостя с тремя представленными вариантами, гораздо красивее и нагляднее чем авторский.
Вы правы как никто другой!!!
Есть вариант куда проще.
https://yadi.sk/i/rDgyEg2jeJMJW
Странное деление, визуально кажется неправильным
Отсечь от каждого из трех нижних квадратов по 1/6 будет самым рациональным решением.
Да тут бесконечное количество решений. Возьмите любую прямую, пересекающую фигуру. Дальше нужно поворачивать линию в сторону той части, что имеет большую площадь. Так как функция изменения площади при таком повороте линии непрерывна, наступит момент, когда обе площади равны.
Если все 5 квадрата делить на 4~~
Будеть 20 квадрата ~~~,
Нам нужен 10~~~
Итак 5х 4 треугольник(верхн. Лев.уг.1 начало,
Конец--- нижн. Прав.уг.19
2__вариант__~~~
Вверх.прав.уг.1~~нижн. Прав.уг.18(трапеция 1на 4 _h=4ед~~~
Вверх. Прав.3 ~~вниз.прав.уг.16~~
И так далее~~~
S=(4х5)/2~
S=(1+4)x4/2
S=(2+3)x4/2
Хорош,,,,,,12вверх.прав. До 15вверх.лев.(8 целых и 4 половинки)~
~~~спасибо~~~~
А изв. Ещё 1 способ ,
Мне он больше понравился, ,
Центр тяжести 6 квадратов,
(точка пеьесеч. Диаглналов) и
Точка(центр 6-ого квадрата присоединит с центром большим(3*2),
Метод определения линия под центрами тяжести квадратов до удаления 6-ого квадрата,
Спасибо
1. Достороим фигуру до полноценного прямоугольника и получим шестой квадрат.
2. Находим центр полученного прямоугольника, состоящего из 6-ти квдратов, путем пересечения диагоналий. Назовем ее А.
3. Находим центр полученного шестого квадрата путем пересечения диагоналей. Назовем ее B.
4. Проводим прямую через точки А и В. Эта прямая разделит фигуру из 5-ти квадратов точно пополам.
Нужно провести линию через центр 4-х квадратов и центр 5-го квадрата.Это 2-й вариант ответа
Задача про торт(см выше).решение то же!