Павел Петрович с супругой прибыли на встречу с тремя другими супружескими парами. Так как некоторые из гостей не были знакомы друг с другом, последовали рукопожатия между незнакомыми (никто не пожимал руку ни своему супругу (супруге), ни себе). Когда все оказались знакомыми, Павел Петрович спросил у остальных семи присутствующих, сколько рукопожатий они сделали. Оказалось, что все пожали разное число рук.
Сколько рук пожал Павел Петрович?
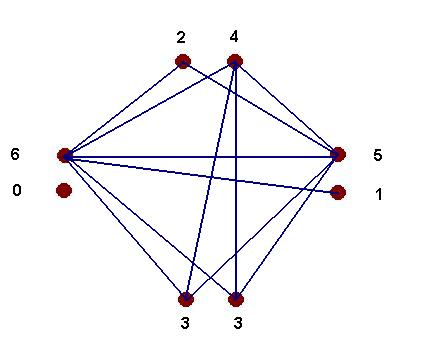
Ответ: Если все пожали разное число рук, причем максимальное число незнакомых равно 6, значит 7 человек пожали от 0 до 6 рук, а Павел Петрович столько же, сколько кто-то другой из гостей. Единственный вариант, когда семь гостей пожимают разное число рук от 0 до 6, при этом оставшийся пожимает 3 руки.
Обсуждение задачи на форуме: На вечеринке

Комментарии
Что то, меня смущает ваш ответ, на данную задачу!
Я понимаю по иному:
Всего человек - 8 из них все пожали разное число рук. Теперь от сюда вычтем 2 так как, не жали рук своим спутникам(цам) и себе. И того имеем - 6 различий. Следовательно не сложно допустить:
1-й пожал - 1 руку;
2-й пожал - 2 руки;
3-й пожал - 3 руки;
4-й пожал - 4 руки;
5-й пожал - 5 рук;
6-й пожал - 6 рук;
7-й пожал - 0 рук;
8-й пожал - 0-6 рук.(Это и есть П.П.)
Вот какое дело получается! 7 человек пожало от "0" до "6" рук. Тогда получается что и П.П. пожал - от "0" до "6" Так как по условию задачи, не сказано(и не может быть сказано), что П.П. тоже имел отличное от остальных, количество рукопожатий. Следовательно:
- закрывайте глаза и ткните в любое число от "0" до "6" и вы будете правы!
А подумать?
4
он пожал 3 руки, так как женщинам руки не жмут, идиоты
Аха, а остальные как жали? 4 рукопожатия тогда как сделали?
Павел Петрович пожал 7 рук, т.к. был знаком со всеми, но просто поздоровался!
ПП пожал 8 рук т.к. был большой шутник и поздоровался сам с собой
Не соглашусь с вами, господин "и-т"! В деловой обстановке, женщинам пожимают руку(и то даже более приемлемо). А ваши возгласы - попытка привлечь к себе внимание, но ведь можно то сделать иным способом. Без выпендрежа! :-)
Согласно теории графом, ответ может бить только 1, 3 или 5
А думать не надо!
Вообще то, условие задано не верно. Как мы видим из схемы "рукопожатий" два человека пожали одинаковое число рук, что противоречит условию задачи, а именно: "Оказалось, что все пожали разное число рук".
Фраза "Оказалось, что все пожали разное число рук" относится только к остальным семи присутствовавшим (исключая Павла Петровича)
"Павел Петрович с супругой прибыли на встречу с тремя другими супружескими парами."
следовательно П.П. со всеми знаком, т.к. он с ними пришел
ответ : 0
Я тоже так считаю, что 0.
ваш ответ кажется неверным.если сказанно что все оказались знакомы, значит все должны были пожать друг другу руки, а на схеме есть те кто не пожал некоторым руки.. так значит, они незнакомы? или просто услышав имя, решили что познакомились?)
в целом, задача плохо сформулированна.
Довольно интересная и несложная задача. То, что пишут в комментариях, разочаровывает. Неужели трудно хоть немного подумать? Зачем же заходить тогда на подобные сайты?
о! моя задачка! :)
Если судить по правилам этикета,то Павет Петрович пожал три руки мужчинам,а женщинам он судя по всему должен был ручку поцеловать.
ответ не верен, в условии сказано "все пожали" вариант 0 пожатий отпадает, логично?
"...Так как некоторые из гостей не были знакомы друг с другом...", к чему эта фраза в условии!?, получается что "некоторые" уже были знакомы? и какое количество этих "некоторых" гостей была знакома!?
Очень классная задачка, а так ведь реально и получается!!! Сам сначала не догнал, но, народ, попробуйте сами нарисовать, тогда увидите, что задачка абсолютно адекватная! Спасибо за задачку!
А те три пары, были ему знакомы? Может он им руки при встрече пожал, а потом уже в гости пошлиЁ ониже вместе приехали?
4 раз
могу предложить другую интерпритацию ответа:
1й ч-к - 1 руку : 6
2й ч-к - 2 руки : 6 5
3й ч-к - 3 руки : 6 5 4
4й ч-к - 4 руки : 6 5 3 8(т.к. себе нельзя,а 1 и 2 уже выпадают)
5й ч-к - 5 рук : 6 4 3 2 8(т.к. себе нельзя,а 1 уже выпадает)
6й ч-к - 6 рук : 5 4 3 2 1 8(т.к. себе нельзя,а не хватает одного пожатия)
7й ч-к - 0 рук :
8й ч-к - Х рук : 6 5 4
Следовательно П.П. пожал 3 руки.
удивительным образом такое объяснение более лаконично и доходчиво, чем кажущееся мне более очевидным математическое (при разбросе от 0 до 6 в каждой паре сумма пожатий будет равна 6, поэтому остаётся только вариант 3+3).
А никого не смутило наличие двух одинаковых чисел на графе?..
Или вот это:
В задаче : "Оказалось, что все пожали разное число рук."
В ответе : "а Павел Петрович столько же, сколько кто-то другой из гостей."
А еще есть такая штука "однозначность условий".
П.П. пожал 3 руки, т.к. дамам жать руки он не мог, а мужчин соответственно мог и не знать, а руку пожать при знакомстве должен.
Ответ: 3 рукопожатия было у Павла Петровича.
Решение: в условии есть 2 ключевых момента:.1. каждый из 8-ми лиц мог пожать не более 6 рук, т.к. свою руку и руку своей супруги (-га) пожать не мог; 2. на вопрос П.П. семеро ответили, что они пожали разное число рук. Из вышесказанного выходит, что 7 чел имели 7 различных вариантов рукопожатия - 1, 2, 3, 4, 5, 5, 0 рук. Значит, всего пожимающих др другу руки лиц было 7 вместе с П.П, т.к. один - не пожимал ничьей руки. Так вот, 7 чел имели уже не 6, а 5 вариантов рукопожатий, т.к. себя и супругу (-га) не в счёт. Но ведь кто-то пожимал 6 рук? Да, это возможно в одном случае - этот кто-то муж (жена) 0 (не пожимавшего руки человека). Значит, 6 --- 0 = пара (муж и жена). При 6 рукопожатиях каждому досталось 1 пожатие. Теперь один вновь выпадает из звена - тот, у кого всего одно рукопожатие. Осталось 6 лиц, у каждого 4 варианта рукопожатия ( нельзя себе и супруге). Но кто-то пожал 5 рук? Да, это - муж 1 ( чел, пожавший одну руку). Теперь каждый получил второе рукопожатие (и наш ПП тоже). Один вновь выбывает - тот, который пожал 2 руки. Теперь их 5 чел. У каждого 3 варианта рукопожатия. Но один пожал 4 руки - это муж выбывшего из круга 2 (лица с 2-мя рукопожатиями). Все получили по одному дополнительному рукопожатию. Итак, у нашего П.П. уже 3 рукиопожатия. Так вот, определены лица, пожавшие 0, 1, 2, 3, 4, 5, 6 рук. Наш П.П. пожал ст рук, ск пожал их один из 7-ми лиц. Поскольку на 3 рукопожатии все определились, то у П.П. в итоге оказалось 3 пожатых руки. Вот. Непмного долго, постаралась логично разобраться в задачке. Так и пары можно определить. Они соответствуют схеме. 6 пара 0, 5 пара 1, 4 пара 2, 3 пара 3. Мудро, жена П.П. не знала стольких, скольких не знал её муж :).
всего на вечеринке 8 человек,п.п. ответило 7 человек о разном кол-ве рукопожатий,из этого никак не получается вывода,что кто-то не пожал ниодной руки,т.к. сам себе п.п. на вопрос не отвечал,а остальные семь пожимали руки,хоть и разное кол-во
Если они встретились, то минимум трое из них должны были быть знакомы - значит разное число рукопожатий. Неизвестно
классная задача
Свингеры
Че за бредовый ответ? Все ведь просто: Петрович встретился с тремя парами - значи пожал руку трем мужмкам. Если пожал меньше трех раз, значит либо просто виделся(а не встретился), либо пары были не разнополые.
там не было сказано, что Петрович не был знаком с остальными, а значит зачем ему было жать руку? разве только поздароваться
отличная задачка
Занятная задачка, хотя и не сложная. Ставлю пять!!!
в условии не плохо бы выделить, что руки пожимали не только мужики, но и М с Ж, или Ж с Ж, т.к. в россии такое не принято, а задачу без этого не решить.
По приведённым условиям задача не имеет решения... Читаем: "Павел Петрович спросил у остальных семи присутствующих, сколько рукопожатий они сделали. Оказалось, что ВСЕ пожали разное число рук". Если написано "все", значит все, включая Павла Петровича (8 человек) пожали разное количество рук, условие про супругов и себя, которое ставит диапазон от 0 до 6 (всего 7 вариантов), исключает ответ, удовлетворяющий всем условиям задачи. Если бы было написано "они" или "все они", или хоть как-то указано, что Павел Петрович в число "всех" не входит, я бы согласился, что задача имеет решение, но именно в приведённой формулировке категорически нет.