Человек вышел из некоторой точки на поверхности земного шара, прошел 10 км на на север, затем 10 км на восток, затем 10 км на юг и 10 км на запад и вернулся в исходную точку. Для каких точек земного шара возможно подобное путешествие?
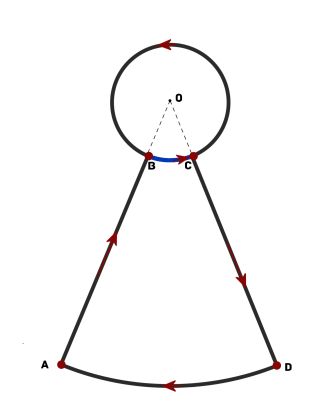
Ответ: Первый ответ - все точки параллели, лежащей на 5 км южнее экватора. Второй вариант немного посложнее: человек выходит из точки A, доходит до B, далее идет по параллели, описав полный круг вокруг Северного полюса и пройдя дополнительно по дуге BC. У точки C он поворачивает на юг и идет до D. И возвращается в точку A

Комментарии
а можно поподробней с ответом?
Земля имеет форму шара. Имхо)
Если человек будет ходить только в северном полушарии, то когда он идет на восток 10 км, он уйдет намного дальше чем когда будет идти на запад те же 10 км.
Его путь будет в виде трапеции, а значит чтобы вернуться в исходную точку ему нужно пройти больше 10 км на запад, чтобы вернуться в исходную точку.
Только когда он ходит возле экватора, его путь будет в виде квадрата ( с двумя выпуклыми сторонами).
Как-то так.
Не совсем так. Правильнее сказать, что расстояния между долготами чем севернее, тем короче, так как чем севернее параллель, тем ее длина меньше. Соответственно, последний отрезок всегда немного не доходит то точки старта. Если перенести проекцию нашей задачи на плоскость, то получится трапеция с немного бОльшим основанием.
Вы видно обкурились все вместе, о каких трапециях речь?
Здесь вообще в условии мера длинны указана, какая разница какой рисунок она будет образовывать при проэкции на плоскую поверхность?
Тем более, что в масштабах земного шара относительно десяти километров, эта проэкция будет едва ли отличима от идеального квадрата.
то есть если я не на экваторе а в саратове,то как не крути не смогу прийти по ровному 40 км. квадрату в исходную точку? Если это так то я просто поражен ведь это изменяет всё моё представление ....
Ты в следующий раз загадки формулируй лучше
ну пусть и изменяет, но это ведь действительно так
Решение верно чисто математически, на практике невязка будет очень малой.
10 км составляют 1/2000 от меридиана, т.е. дугу в пи/2000, примерно 0,006. радиан. Дуга параллели пропорциональна косинусу широты. Относительное приращение будет примерно равно тангенсу широты га разность углов. Для широты 45 градусов тангенс равен 1, так что изменение расстояния примерно равно 10 км•0,006 = 60 м.
Довольно маленькое расстояние, чем можно померить километры настолько точно?
у Я.Перельмана эта задача дается для 500 км, а не для 10.
Ошибка в счёте, на самом деле число примерно в 4 раза меньше.
при чём тут экватор??? ответ- все точки кроме северного полюса
я думаю все точки экватора
Если мыслить реально а не примитивно, то 10 км в масштабе земли-нет ничего. На этом участке может быть и гора и овраг и равнина. По сути дела данная ситуация возможна во всех точках, где длина пути по параллелям и меридианам равна 10 км, а форма поверхности может быть любая. Например 5 ям на одной параллели и 5 холмов на другой и так далее, но длина пути с учетом всех неровностей должна быть 10 км в каждом направлении.
Согласен с ответом. Еще человек может выйти на любой точки полюса. Тогда он будет описывать "треугольник", а в точке полюса ему нужно кружиться волчком 10 км, держа ноги на ширине плеч и описывая круг, и каждой ногой пройти по 5 км. Если ширина его плеч 40 см, то он должен будет совершить 3979 оборотов вокруг своей оси.
Добавлю свои пять копеек.
По-началу вообще не понял задачу. Ну да, земля типа круглая, но в условиях данной задачи задумываться об этом стоит лишь вблизи от экватора. В обычных же широтах (в той же Москве, к примеру) идеального квадрата не получится, т.е. не вернется человек ИМЕННО в ту точку, откуда вышел, но смещение будет настолько маленьким, что им можно пренебречь.
Тут правильно народ писал - было бы не 10 километров в условии, а 500 - тогда можно было бы задуматься.
Оригинал задачи звучит так. Вертолёт вылетает из Ленинграда (1985г) и летит строго на север 250 км. Потом на восток 250 и тд. Не долетает около 40 км по памяти. Но были и матем. доказательства.