Один заядлый спорщик постоянно выигрывал, как правило, казалось бы, сложные пари. Он описывал на листе бумаги событие, которое произойдет или не произойдет в течение ближайших 5 минут, и, перевернув лист, клал его на стол. В свою очередь его соперник на другом листе бумаги писал слово "Да", если считал, что неизвестное ему описанное на листке событие произойдет, и "Нет" - если не произойдет. Через 5 минут записки зачитывались. Если соперник угадал, он получал 100$, если не угадал, то выплачивал спорщику 1$. Что писал спорщик, если известно, что он ни разу не проиграл?

Перед Вами пять коробочек: белая, черная, красная, синяя и зелёная. Также есть по два шарика для каждого из цветов. В каждой коробочке лежит по два шарика, причём цвета коробочки и шариков могут не совпадать. Также известно, что:
1. Ни один шарик не лежит в коробочке того же цвета, что и он сам;
2. В красной коробочке нет синих шариков;
3. В коробочке нейтрального цвета (то есть белого или чёрного) лежит один красный и один зелёный шарик;
4. В чёрной коробочке лежат шарики холодных тонов (зелёный и синий цвета);
5. В одной из коробочек лежат один белый и один синий шарик;
6. В синей коробочки находится один чёрный шарик.
Какого цвета шарики лежат в каждой коробочке? 

Учитель начертил на классной доске четырехугольник. Янош утверждал, что это квадрат. Имре считал, что четырехугольник - трапеция. Мария думала, что на доске изображен ромб. Ева назвала четырехугольник параллелограммом. Выслушав каждого и внимательно изучив свойства четырехугольника, учитель установил, что ровно 3 из 4 суждений истинны и ровно 1 суждение ложно.
Какой четырехугольник начертил учитель на классной доске?

В одном классе ученики разделились на две группы. Одни должны были всегда говорить (и писать) только правду, а другие - только неправду. Все ученики класса написали сочинение на свободную тему, которое должно было заканчиваться фразой "Всё здесь написанное - правда" или "Всё здесь написанное - ложь". В классе было 17 правдолюбцев и 18 лжецов. Сколько получилось сочинений с утверждением о правдивости написанного? 

Сегодня не воскресенье, а завтра не среда. Вчера была не пятница, а позавчера был не понедельник. Завтра не воскресенье, и вчера было не воскресенье. Послезавтра не суббота и не воскресенье. Вчера был не понедельник, и не среда. Позавчера была не среда, а завтра не вторник. Да, и сегодня не среда. Какой же сегодня день недели, если учесть, что одно утверждение в списке - ложно? 

На одном крупном банкете произошел инцидент - какого-то гостя попытались отравить.
Всех сразу эвакуировали. Когда прибыли полицейские, они увидели на огромном столе стаканы с вином, и уже никто из свидетелей не помнил, где сидел потерпевший. Но было точно известно, что отравленный стакан - один, а всего стаканов было от сотни до двухсот.
Нужно было определить, какой стакан отравлен.
Эксперт сказал, что не имеет смысла проверять каждый стакан - это дорого и долго.
После того, как эксперт сосчитал стаканы , он сказал:
- Мы будем брать небольшое число жидкости из нескольких стаканов, и проверять смесь, таким образом, нам не понадобится и десяти проверок, чтобы выявить отравленный стакан!Но при этом, взяв один стакан, он заявил, что надо исследовать его первым - и это не будет растратой попыток впустую.
Свою оптимальную методику он наметил исходя из подсчитанного им числа стаканов.
Исходя из этих данных можно заключить, какое точное число стаканов стояло на столе. 

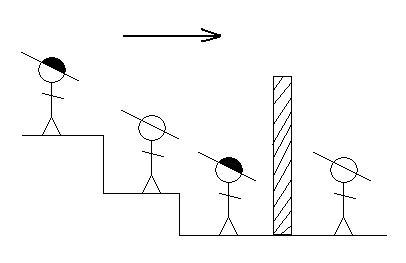
На этом рисунке 4 человека, двое из них в черных шляпах и двое - в белых.

Перегородка - это стена, через которую ничего не видно.

Слева направо: 1-й человек видит 2-го и 3-го, 2-й видит 3-го, 3-й видит стенку, 4-й вообще ничего не видит.

Они знают, как они стоят, знают, что есть 2 черные и 2 белые шляпы.

Каждого из них спрашивают: "Знаешь ли ты, в какой ты шляпе?"

Допускается два варианта ответа: "Да, знаю, я в ... шляпе" либо "Нет. Не знаю"

Кто первым сможет ответить, в какой он шляпе?

Четыре ангела сидели на рождественской елке среди украшений. У двоих нимбы были синего цвета, у двоих – желтого. Ангелы не знают, у кого какой нимб, но знают, кто кого может видеть (см. ниже). Ни один из них не может видеть сидящих над ним, но каждый может слышать друг друга. Ангел A, сидящий на самой верхней ветке, может видеть ангелов B и C, которые сидят ниже него. Ангел B может видеть ангела C, который сидит веткой ниже. Ангел C не может видеть никого, потому что ангел D спрятался за деревом так, что никто не может видеть его, но и он сам никого не может увидеть.
Кто из них может первым догадаться о цвете своего нимба и сказать об этом остальным?

Однажды король решил выяснить, кто из двух придворных мудрецов мудрее. Для этого он устроил турнир со следующими условиями:
требовалось найти два наименьших целых положительных числа, заданных через их сумму и сумму их квадратов.

Первому мудрецу сообщили сумму чисел, второму - сумму квадратов. Между мудрецами состоялся следующий диалог:
- Пока что я не знаю этих чисел, начал первый мудрец.
- Я тоже не в состоянии их вычислить, - признался его противник
- А вот теперь я догадался! - вскричал первый и назвал правильный ответ.
Что это были за числа?